Аналитик геометрия

Аналити́к геоме́трия — геометрияның, геометрик фигуралар һәм уларҙың үҙсәнлектәре алгебра саралары менән өйрәнелгән бүлеге.

Декарт координаталар системаһы

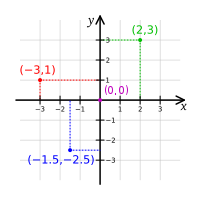
Был ысулдың нигеҙендә координаталар ысулы тип аталған, беренсе башлап Декарт 1637 йылда ҡулланған ысул ята. Һәр геометрик бәйләнешкә был ысул, фигураның йәки есемдең координаталарын бәйләүсе ниндәйҙер тигеҙләмәне ярашлы ҡуя. Бындай геометрик үҙсәнлектәрҙе «алгебралаштырыу» ысулы үҙенең универсаль булыуын иҫбат итте һәм күп тәбиғәт фәндәрендә һәм техникала емешле ҡулланыла. Математикала аналитик геометрия шулай уҡ геометрияның башҡа бүлектәре өсөн нигеҙ булып тора — мәҫәлән, дифференциаль, алгебраик, комбинаторлы һәм иҫәпләү геометрияһы.

Тарихи белешмә

Координаталар һәм кәкере һыҙыҡ тигеҙләмәһе идеяһы боронғо гректарға ла ят булмай. Архимед, һәм бигерәк тә Аполлоний Пергский, үҙҙәренең яҙмаларында конус киҫелештәре симптомдарын килтерәләр, улар ҡайһы бер осраҡтарҙа беҙҙең тигеҙләмәләр менән тап киләләр. Әммә был идея ул осорҙа, боронғо грек алгебраһының түбән кимәле һәм тура һыҙыҡ менән әйләнәнән башҡа кәкере һыҙыҡтар менән артыҡ ҡыҙыҡһыныу булмау сәбәпле, артабан үҫеш алмай.

Аҙаҡ Европала Николай Орезмский (XIV быуат) координаталы һүрәтләү (ваҡытҡа бәйле функция өсөн) ҡуллана, ул координаталарҙы, географик координаталарға оҡшаш рәүештә, оҙонлоҡ һәм киңлек тип атай. Был ваҡытҡа координаталар тураһында үҫешкән төшөнсә астрономияла һәм географияла булған була. Хәл иткес аҙым, Виет (XVI быуат) тигеҙләмәләрҙе яҙыу өсөн символлы тел төҙөгәндән һәм системалы (символик) алгебраға баш һалғандан һуң яһала.

1637 йылдар тирәһендә Ферма Мерсенн аша «Введение в изучение плоских и телесных мест» мемуарын тарата, унда (Виет символикаһында) 2-се тәртиптәге төрлө кәкре һыҙыҡтарҙың тура мөйөшлө координаталарҙа тигеҙләмәләрен яҙып сыға. Тигеҙләмәләрҙең күренешен ябайлаштырыу өсөн ул координаталарҙы үҙгәртеүҙе киң ҡуллана. Ферма, асыҡ итеп, таҙа геометрик ысулға ҡарағанда яңы ҡараш ни тиклем ябайыраҡ һәм емешлерәк икәнен күрһәтә. Ләкин Ферманың мемуары киң билдәлелек яуламай. Декарттың шул уҡ 1637 йылда баҫылып сыҡҡан, Фермаға бәйһеҙ рәүештә һәм күпкә тулыраҡ шул уҡ идеяларҙы үҫтергән «Геометрияһының» йоғонтоһо күпкә ҙурыраҡ була.

Декарт геометрияға кәкре һыҙыҡтарҙың киңерәк класын, шул иҫәптән «механик» (спираль һымаҡ трансцендент) индерә, һәм һәр кәкре һыҙыҡты билдәләүсе тигеҙләмә бар тип иғлан итә. Ул алгебраик кәкре һыҙыҡтар өсөн тигеҙләмәләр төҙөй һәм уларҙы классификациялай (һуңғараҡ Ньютон тарафынан төплө итеп киренән эшләнә). Декарт кәкре һыҙыҡтарҙың төп характеристикалары координаталар системаһын һайлауға бәйле түгеллеген һыҙыҡ өҫтөнә ала, ләкин иҫбат итмәй.

Декарттың координаталар системаһы хәҙерге менән сағыштырғанда әйләндереп ҡуйылға була (ординаталар күсәре горизонталь), һәм тиҫкәре координаталар ҡаралмай. «абсцисса» һәм «ордината» терминдары һирәкләп төрлө авторҙарҙа осрай, ләкин тик Лейбниц XVII быуат аҙағында «координата» термины менән бергә уларҙы киң ҡулланыуға индерә. «Аналитик геометрия» атамаһы XVIII быуаттың иң аҙағында нығына.

Декарт «Геометрияға» яңы ысулдың сикһеҙ ҡеүәтен сағылдырыусы күп миҫалдар индерә, һәм боронғоларға билдәле булмаған күп һөҙөмтәләргә ирешә. Арауыҡта ҡулланылырға мөмкин булыуын да телгә ала, тик был идея унда үҫеш алмай.

Декарттың аналитик ысулын шунда уҡ ван Схоутен, Валлис һәм башҡа күп күренекле математиктар ҡулланыуға алалар. Улар «Геометрияның» идеяларына аңлатма бирәләр һәм тулыландыралар, уның етешһеҙлектәрен төҙәтәләр, яңы ысулды башҡа мәсьәләләрҙә ҡулланалар. Мәҫәлән, Валлис беренсе тапҡыр конус киҫелештәрен яҫы кәкре һыҙыҡ һымаҡ ҡарай (1655 йыл), шуның менән бергә, Декарттан айырмалы рәүештә, ул инде тиҫкәре абсциссаларҙы һәм ҡыя мөйөшлө координаталарҙы ҡуллана.

Ньютон үҙенең анализ буйынса хеҙмәттәрендә координаталар ысулына таянып ҡына ҡалмай, ә Декарттың геометрик тикшеренеүҙәрен дауам итә. Ул 3-сө тәртиптәге кәкре һыҙыҡтарҙы классификациялай, уларҙы 4 типҡа һәм 58 төргә айыра; һуңғараҡ ул тағы ла 14 төр өҫтәй. Был һөҙөмтәләр яҡынса 1668 йылда алына, «Оптика»һы менән бергә 1704 йылда баҫылып сыға. Ньютондың координаталар системаһы хәҙергенән бер ни менән дә айырылмай инде. Һәр кәкре һыҙыҡ өсөн диаметр, симметрия күсәре, түбәһе, үҙәге, асимптотаһы, айырым нөктәләре һәм башҡалар билдәләнә.

Үҙенең «Башланғыстарында» Ньютон, координаталар һәм сикһеҙ бәләкәй төшөнсәләрен ҡулланмай, бөтәһен дә боронғолар алымында иҫбатларға тырышҡан; ләкин яңы ысулдың бер нисә ҡулланышы унда шулай ҙа бар. Аналитик геометрия уның «Дөйөм арифметикаһында» ҙур роль уйнай, әммә Ньютон күп осраҡта иҫбатлауҙар килтереүҙе кәрәк тип тапмай, бының менән аңлатма биреүселәрҙең ҙур армияһын оҙаҡ йылдарға эш менән тәьмин итә.

XVIII быуаттың беренсе яртыһында башлыса юғары тәртиптәге алгебраик кәкре һыҙыҡтарҙы өйрәнеү дауам итә; Стирлинг Ньютон күрмәгән яңы 4 типты асыҡлай, айырым нөктәләр асыҡлана һәм классификациялана.

Клеро 1729 йылда Париж академияһына «Исследования о кривых двоякой кривизны» хеҙмәтен тәҡдим итә. Был китап асылда өс геометрик фәнгә башланғыс бирә: арауыҡта аналитик геометрияға, дифференциаль геометрияға һәм һыҙма геометрияға.

Кәкре һыҙыҡтарҙың һәм йөҙҙәрҙең дөйөм һәм бик йөкмәткеле теорияһын (башлыса алгебраик) Эйлер тәҡдим итә. Үҙенең «Введении в анализ бесконечно малых» хеҙмәтендә (1748) ул 4-се тәртиптәге кәкре һыҙыҡтарҙың классификацияһын бирә һәм кәкрелек радиусын нисек асыҡларға икәнен күрһәтә. Унда, уңайлы булған урында, ул ҡыйыш мөйөшлө координаталар йәки поляр координаталар ҡуллана. Айырым бүлек алгебраик булмаған кәкре һыҙыҡтарға арнала.

XVIII быуаттың икенсе яртыһында аналитик геометрия, үҫешкән анализдың ҡеүәтле ярҙамын алып, яңы үрҙәр яулай (Лагранж, Монж), әммә инде дифференциаль геометрияның аппараты һымаҡ ҡарала.

Бүлектәре

Аналитик геометрияның төп бүлектәре (Н. В. Ефимовтың китабына ярашлы).

• Координаталар системаһы
  • Тура мөйөшлө координаталар системаһы
  • Поляр координаталар системаһы
  • Координаталарҙы үҙгәртеү
• Һыҙыҡлы алгебра элементтары
  • Векторҙар өҫтөндә һыҙыҡлы ғәмәлдәр
  • Векторҙарҙың ҡабатландығы
  • Матрицалар һәм улар өҫтөндә ғәмәлдәр
  • Билдәләүселәр
  • Кире матрица һәм матрица дәрәжәһе
  • Һыҙыҡлы алгебраик тигеҙләмәләр системалары
• Беренсе тәртиптәге кәкре һыҙыҡтар
  • Яҫылыҡта тура һыҙыҡ
  • Арауыҡта тура һыҙыҡ һәм яҫылыҡ
• Икенсе тәртиптәге кәкре һыҙыҡтар
  • Әйләнә
  • Конус киҫелеше
• Спираль
• Арауыҡ есемдәре
  • Икенсе тәртиптәге йөҙҙәр
  • Цилиндр
  • Сфера
  • Конус
  • Шар

Шулай уҡ ҡарағыҙ

• Алгебраик геометрия
• Дифференциаль геометрия
• Һыҙыҡлы алгебра
• Векторлы иҫәпләү

Әҙәбиәт

• Бортаковский А. С., Пантелеев А. В. Аналитическая геометрия в примерах и задачах: Учеб. пособие. — М.: Высш. шк., 2005. — 496 с. (Серия «Прикладная математика»).
• Веселов А. П., Троицкий Е. В. Лекции по аналитической геометрии. — СПб.: Лань, 2003. — 160 с.
• Делоне Б. Н., Райков Д. А. Аналитическая геометрия, в двух томах. — М., Л.: Гостехиздат, 1948, 1949.
• Ильин В. А., Позняк Э. Г. Аналитическая геометрия. — М.: ФИЗМАТЛИТ, 2002. — 240 с.
• История математики под редакцией А. П. Юшкевича в трёх томах.
  • История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I.
  • Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.
  • Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
• Канатников А. Н., Крищенко А. П. Аналитическая геометрия. — М.: Издательство МГТУ им. Н.Э. Баумана, 2002. — 388 с. — ISBN 5-7038-1671-8.
• Мордухай-Болтовской Д. Д. Из прошлого аналитической геометрии // Труды института истории естествознании Акад. наук СССР, 1952, т. 4, с. 217-235.
• Погорелов А. В. Аналитическая геометрия. — 3-е изд.. — М.: Наука, 1968. — 176 с.