Трапеция

Трапе́ция (бор. грек. τραπέζιον — «бәләкәй өҫтәл» һүҙенән τράπεζα — «өҫтәл» һүҙенән ) — ике яғы параллель булған ҡабарынҡы дүртмөйөш. Йыш ҡына трапеция билдәләмәһендә ҡалған ике яғы параллель булмаҫҡа тейеш тигән шарт өҫтәйҙәр. Параллель булған ҡапма-ҡаршы яҡтары трапецияның нигеҙҙәре тип аталалар, ә ҡалған ике яғы — эргә яҡтары тип атала. Урта һыҙығы — эргә яҡтарының урталарын тоташтырған киҫек.

Трапеция
Ҡайҙа өйрәнелә	геометрия
Грань политопа	ҡабырға
Вики-проект	Проект:Математика[d]
Трапеция Викимилектә

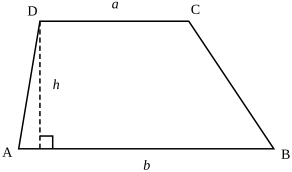
Билдәләмәнең төрҙәре

Трапецияның икенсе билдәләмәһе лә бар.

Трапеция — ике яғы параллель булған ҡабарынҡы дүртмөйөш. Был билдәләмәгә ярашлы, параллелограмм һәм тура дүртмөйөш — трапецияның айырым осраҡтары. Түбәндә килтерелгән формулалар трапецияның ике билдәләмәһе өсөн дә дөрөҫ.

Бәйләнгән билдәләмәләр

Трапецияның элементтары

Трапецияның диагоналдәре киҫешкән нөктә, уның эргә яҡтарының дауамы киҫешкән нөктә һәм нигеҙҙәренең урталары бер тура һыҙыҡта яталар

• Параллель булған ҡапма-ҡаршы яҡтары трапецияның нигеҙҙәре тип аталалар.
• Ҡалған ике яғы трапецияның эргә яҡтары тип аталалар.
• Трапецияның эргә яҡтарының урталарын тоташтырған киҫек трапецияның урта һыҙығы тип атала.

Трапецияның төрҙәре

• Эргә яҡтары тигеҙ булған трапеция тигеҙ эргәле трапеция тип атала (һирәгерәк тигеҙ ҡабырғалы или равнобочной трапецией).
• Эргә яғы эргәһендәге мөйөштәре тура булған трапеция тура мөйөшлө трапеция тип атала.

• 
  Тигеҙ эргәле трапеция
• 
  Тура мөйөшлө трапеция

Уртаҡ үҙсәнлектәре

Төп сығанаҡ:

• Трапецияның урта һыҙығы нигеҙҙәренә параллель һәм уларҙың ярымсуммаһына тигеҙ.
• Диагоналдәренең уртаһын тоташтырған киҫек нигеҙҙәренең ярым айырмаһына тигеҙ һәм урта һыҙыҡта ята.
• (Дөйөмләштерелгән Фалес теоремаһы). Мөйөштөң яҡтарын киҫеүсе параллель тура һыҙыҡтар мөйөштөң яҡтарынан пропорциональ киҫектәр киҫеп алалар.
• Әгәр трапецияның нигеҙҙәре оҙонлоҡтары суммаһы уның эргә яҡтарының оҙонлоҡтары суммаһына тигеҙ булһа, был трапецияға әйләнә ҡамарға мөмкин.
• Трапеция диагоналдәренең киҫешеү нөктәһе аша үткән һәм нигеҙҙәренә параллель булған киҫек был нөктә менән урталай бүленә һәм ${\frac {2xy}{x+y}}$ трапеция нигеҙҙәре оҙонлоҡтарының гармоник уртаһына тигеҙ (Бураков формулаһы).
• Трапецияның диагоналдәре киҫешкән нөктә, уның эргә яҡтарының дауамы киҫешкән нөктә һәм нигеҙҙәренең урталары бер тура һыҙыҡта яталар.
• Әгәр трапецияның теләһә ҡайһы нигеҙе эргәһендәге мөйөштәренең суммаһы 90°-ҡа тигеҙ булһа, нигеҙҙәренең урталарын тоташтырған киҫек уларҙың ярым айырмаһына тигеҙ.
• Трапецияның диагоналдәре киҫешкәндә нигеҙҙәрендә ятҡан өсмөйөштәр оҡшаштар.
• Эргә яҡтарында ятҡан өсмөйөштәр тигеҙ ҙурлыҡта.
• Әгәр нигеҙҙәренең сағыштырмаһы $K$-ға тигеҙ булһа, ул саҡта нигеҙҙәрендә ятҡан өсмөйөштәрҙең майҙандары сағыштырмаһы $K^{2}$ тигеҙ.
• Трапецияның бейеклеге түбәндәге формула менән билдәләнә:

$h={\sqrt {c^{2}-{\frac {1}{4}}\left({\frac {c^{2}-d^{2}}{b-a}}+b-a\right)^{2}}}$

бында $b$ — ҙур нигеҙе, $a$ — бәләкәй нигеҙе, $c$ һәм $d$ — эргә яҡтары.

• Трапецияның диагоналдәре $d_{1}$ һәм $d_{2}$ яҡтары менән түбәндәге нисбәт менән бәйләнгән:

$d_{1}^{2}+d_{2}^{2}=2ab+c^{2}+d^{2}$

Уларҙы асыҡ итеп күрһәтергә була:

$d_{1}=AC={\sqrt {ab+d^{2}+{\frac {b(c^{2}-d^{2})}{b-a}}}}$

$d_{2}=BD={\sqrt {ab+c^{2}-{\frac {b(c^{2}-d^{2})}{b-a}}}}$

Әгәр, киреһенсә, эргә яҡтары һәм диагоналдәре билдәле булһа, ул саҡта нигеҙҙәре түбәндәге формулалар менән күрһәтеләләр:

$a={\sqrt {\frac {(c^{2}-d_{1}^{2})^{2}-(d^{2}-d_{2}^{2})^{2}}{2(c^{2}-d^{2}+d_{1}^{2}-d_{2}^{2})}}}$

$b={\sqrt {\frac {(c^{2}-d_{2}^{2})^{2}-(d^{2}-d_{1}^{2})^{2}}{2(c^{2}-d^{2}-d_{1}^{2}+d_{2}^{2})}}}$

ә билдәле нигеҙҙәре һәм диагоналдәре аша эргә яҡтары түбәндәгесә:

$c={\sqrt {\frac {a(d_{2}^{2}-b^{2})+b(d_{1}^{2}-a^{2})}{a+b}}}$

$d={\sqrt {\frac {a(d_{1}^{2}-b^{2})+b(d_{2}^{2}-a^{2})}{a+b}}}$

Әгәр бейеклеге $h$ билдәле булһа, ул саҡта

$d_{1}={\sqrt {b^{2}+d^{2}-2b{\sqrt {d^{2}-h^{2}}}}}={\sqrt {h^{2}+\left(b-{\sqrt {d^{2}-h^{2}}}\right)^{2}}}$

$d_{2}={\sqrt {b^{2}+c^{2}-2b{\sqrt {c^{2}-h^{2}}}}}={\sqrt {h^{2}+\left(b-{\sqrt {c^{2}-h^{2}}}\right)^{2}}}$

Тигеҙ эргәле трапецияның үҙсәнлектәре һәм билдәләре

Трапеция тигеҙ эргәле була шул саҡта һәм тик шул саҡта ғына, әгәр түбәндәге эквивалентлы шарттарҙың теләһә ҡайһыһы үтәлһә:

• нигеҙҙәренең уртаһы аша үткән тура һыҙыҡ нигеҙҙәренә перпендикуляр (йәғни трапецияның симметрия күсәре булып тора);
• түбәһенән ҙур нигеҙенә төшөрөлгән бейеклек уны, береһе нигеҙҙәренең ярым суммаһына, икенсеһе — нигеҙҙәренең ярым айырмаһына тигеҙ булған киҫектәргә бүләй;
• теләһә ҡайһы нигеҙе эргәһендәге мөйөштәре тигеҙ;
• ҡапма-ҡаршы мөйөштәренең суммаһы 180°-ҡа тигеҙ;
• диагоналдәренең оҙонлоҡтары тигеҙ;
• бындай трапецияны әйләнә менән ҡамарға мөмкин;
• был трапецияның түбәләре булып шулай уҡ ниндәйҙер антипараллелограммдың түбәләре тора.

Бынан тыш

• әгәр тигеҙ эргәле трапецияла диагоналдәр перпендикуляр булһа, ул саҡта бейеклек нигеҙҙәренең ярым суммаһына тигеҙ.

Ҡамалған һәм ҡамаусы әйләнә

[[Категория:Википедия:Сығанаҡтарға һылтанмалары булмаған мәҡәләләр ]]

• Әгәр трапецияның нигеҙҙәре суммаһы эргә яҡтарының суммаһына тигеҙ булһа, ул саҡта был трапецияға әйләнә ҡамарға мөмкин. Был осраҡта урта һыҙыҡ эргә яҡтарының ярым суммаһына тигеҙ (сөнки трапецияның урта һыҙығы нигеҙҙәренең ярым суммаһына тигеҙ).
• Трапецияла уның эргә яғы ҡамалған әйләнәнең үҙәгенән 90° мөйөш аҫтында күренә.
• Әгәр трапеция тигеҙ эргәле булһа, уның тирәләй әйләнә ҡамарға мөмкин.
• Тигеҙ эргәле трапецияны ҡамаусы әйләнәнең радиусы:

$R={\frac {bcd_{1}}{4{\sqrt {p(p-b)(p-c)(p-d_{1})}}}}={\sqrt {\frac {ab+c^{2}}{4-\left({\frac {b-a}{c}}\right)^{2}}}}$

бында $p={\frac {1}{2}}(b+c+d_{1})\,,\,c$ — эргә яҡ, $b$ — ҙур нигеҙе, $a$ — бәләкәй нигеҙе, $d_{1}=d_{2}$ — тигеҙ эргәле трапецияның диагоналдәре.

• Әгәр $a+b=2c$ булһа, ул саҡта тигеҙ эргәле трапецияға радиусы

$r={\frac {h}{2}}={\frac {\sqrt {ab}}{2}}$ булған әйләнә ҡамарға мөмкин.

• Әгәр трапецияға радиусы $r$ булған әйләнә ҡамалһа, һәм ул тейеү нөктәләре менән эргә яҡтарын ике киҫеккә — $v$ һәм $w$ бүлһә — ул саҡта $r={\sqrt {vw}}$.

Майҙан

Бында тап трапецияға хас булған формулалар килтерелгән. Шулай уҡ ҡара: ирекле дүртмөйөштәрҙең майҙандары өсөн формулалар.

• Әгәр $a$ һәм $b$ — нигеҙҙәре һәм $h$ — бейеклек булһа, майҙан формулаһы:

$S={\frac {(a+b)}{2}}h$

• Әгәр $m$ — урта һыҙыҡ һәм $h$ — бейеклек булһа, майҙан формулаһы:

$S=\displaystyle mh$

Иҫкәрмә: Юғарыла килтерелгән ике формула эквивалентлы, сөнки нигеҙҙәренең ярым суммаһы трапецияның урта һыҙығына тигеҙ:

$m={\frac {(a+b)}{2}}$

• Формула, бында $a<b$ — трапецияның нигеҙҙәре, $c$ һәм $d$ — эргә яҡтары:

$S={\frac {a+b}{4(b-a)}}{\sqrt {(a+c+d-b)(a+d-b-c)(a+c-b-d)(b+c+d-a)}}.$

йәки

$S={\frac {a+b}{2}}{\sqrt {c^{2}-{\frac {1}{4}}\left({\frac {c^{2}-d^{2}}{b-a}}+b-a\right)^{2}}}$

• Урта һыҙыҡ $m$ фигураны, майҙандары сағыштырмаһы

${\frac {S_{1}}{S_{2}}}={\frac {3a+b}{a+3b}}$ кеүек булған ике трапецияға бүлә

• Ҡамаусы әйләнәнең радиусы $r$ һәм нигеҙе эргәһендәге мөйөшө $\alpha$ булған тигеҙ эргәле трапецияның майҙаны:

$S={\frac {4r^{2}}{\sin {\alpha }}}$

• Тигеҙ эргәле трапецияның майҙаны:

$S=(b-c\cos {\gamma })c\sin {\gamma }=(a+c\cos {\gamma })c\sin {\gamma }$

бында $c$ — эргә яғы, $b$ — ҙур нигеҙе, $a$ — бәләкәй нигеҙе, $\gamma$ — ҙур нигеҙе менәнэргә яғы араһындағы мөйөш.

• Тигеҙ эргәле трапецияның майҙаны уның яҡтары аша

$S={\frac {a+b}{2}}{\sqrt {c^{2}-{\frac {1}{4}}(b-a)^{2}}}$

Иҫкәрмәләр

Исем

<onlyinclude>

<onlyinclude>